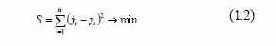|
|
|
Сущность метода наименьших квадратов состоит в отыскании параметров модели тренда, минимизирующих ее отклонение от то- чек исходного временного ряда, т. е.
где У i – расчетные значения исходного ряда; у i – фактические значения исходного ряда; n – число наблюдений. Если модель тренда представить в виде
где a ,a ,...,a – параметры модели; t – время; xi - независимые пе- ременные, то для того, чтобы найти параметры модели, удовлетво- ряющие условию (1.2), необходимо приравнять нулю первые произ- водные величины S по каждому из коэффициентов j a . Решая полу- ченную систему уравнений с k неизвестными, находим значения ко- эффициентов j a . Использование процедуры оценки, основанной на методе наи- меньших квадратов, предполагает обязательное удовлетворение це- лого ряда предпосылок, невыполнение которых может привести к значительным ошибкам.
1. Случайные ошибки имеют нулевую среднюю, конечные дис- персии и ковариации. 2. Каждое измерение случайной ошибки характеризуется нуле- вым средним, не зависящим от значений наблюдаемых переменных. 3. Дисперсии каждой случайной ошибки одинаковы, их величи- ны независимы от значений наблюдаемых переменных (гомоскеда- стичность). 4. Отсутствие автокорреляции ошибок, т. е. значения ошибок различных наблюдений независимы друг от друга. 5. Нормальность. Случайные ошибки имеют нормальное распре- деление. 6. Значения эндогенной переменной х свободны от ошибок измерения и имеют конечные средние значения и дисперсии. |




|
|