где a0 − неизвестный параметр, не зависящий от времени, а ετ − случайный остаток со средним значением, равным нулю, и конечной дисперсией. Как известно, экспоненциально взвешенная скользящая средняя ряда xτ в точке t (λ ) t x с параметром сглаживания (параметром адаптации)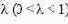                    



определяется формулой



которая дает решение задачи: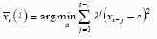



Коэффициент сглаживания λ можно интерпретировать также как коэффициент дисконтирования, характеризующий меру обесценения наблюдения за единицу времени.

Для рядов с «бесконечным прошлым» формула (1.87) сводится к виду



В соответствии с простейшим вариантом метода экспоненциального сглаживания прогноз ˆ1t x для неизвестного значения xt+1 по известной до момента времени t траектории ряда xt строится по формуле



где значение (λ ) t x определено формулой (1.87) или (1.88), соответственно для короткого или длинного временного ряда.



Метод экспоненциального сглаживания можно обобщить на случай полиномиальной неслучайной составляющей анализируемого временного ряда, т.е. на ситуации, когда вместо (1.86) постулируется

---

---