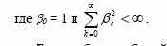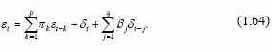|
|
|
Здесь рассматривается набор линейных параметрических моделей. Речь здесь идет не о моделировании временных рядов, а о моделировании их случайных остатков ε t, получающихся после элиминирования (вычитания) из исходного временного ряда xt его неслучайной составляющей (тренда). Следовательно, в отличие от прогноза, основанного на регрессионной модели, игнорирующего значения случайных остатков, в прогнозе временных рядов существенно используется взаимозависимость и прогноз самих случайных остатков. Введем обозначения. Так как здесь описывается поведение случайных остатков, то моделируемый временной ряд обозначим ε t, и будем полагать, что при всех t его математическое ожидание равно нулю, т.е. E ε t ≡ 0. Временные последовательности, образующие «белый шум», обозначим δ t. Описание и анализ рассматриваемых ниже моделей формулируется в терминах общего линейного процесса, представимого в виде взвешенной суммы настоящего и прошлых значений белого шума, а именно
Таким образом, белый шум представляет собой серию импульсов, в широком классе реальных ситуаций генерирующих случайные остатки исследуемого временного ряда. Временной ряд ε t можно представить в эквивалентном (1.62) виде, при котором он получается в виде классической линейной модели множественной регрессии, в которой в качестве объясняющих переменных выступают его собственные значения во все прошлые моменты времени
При этом весовые коэффициенты π 1, π 2,… связаны определенными условиями, обеспечивающими стационарность ряда ε t. Переход от (1.63) к (1.62) осуществляется с помощью последовательной подстановки в правую часть (1.63) вместо ε t−1, ε t−2,… их выражений, вычисленных в соответствии с (1.63) для моментов времени t−1, t−2 и т.д. Рассмотрим также процесс смешанного типа, в котором присутствуют как авторегрессионные члены самого процесса, так и скользящее суммирование элементов белого шума
Будем подразумевать, что p и q могут принимать и бесконечные значения, а также то, что в частных случаях некоторые (или даже все) коэффициенты π или β равны нулю. |




|
|