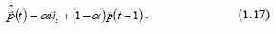|
|
|
Прогнозирование с использованием вероятностных моделей базируется на методе экспоненциального сглаживания. Вероятностные модели по своей сути отличны от экстраполяционных моделей временных рядов, в которых основой является описание изменения во времени процесса. Во временных рядах модели представляют собой некоторую функцию времени с коэффициентами, значения которых оцениваются по наблюдениям. В вероятностных моделях оцениваются вероятности, а не коэффициенты. Пусть определено n взаимно независимых и исключающих событий. В каждом случае наблюдения измеряются в единой шкале, помещаются в (n + 1) ограниченный класс и обозначаются так: x1, x2, …, xn. Событие, связанное с наблюдением x(t), соответствует числу интервалов, в которое это событие попадает, т. е. существует един- ственное значение k, такое, что ( k ) k x < x t ≤ x −1 . И поэтому k-e событие связывается с наблюдением x(t). Рассмотрим метод оценивания вероятностей p (t) n ˆ , связанных с различными событиями ( ) k k x < x t ≤ x −1 . На первом этапе задаются начальные значения различных вероятностей: ˆ (0) k p ; k ≠ 1,2,...,n . Наблюдение х(t) связано с k-м событием следующим образом: если ( ) k k x < x t ≤ x −1 , то строится единичный вектор k ur , (k - 1) компонент которого равен 0 и k-й компонент равен 1. Это может быть k-м столбцом единичной матрицы ранга k. Процесс, реализующий оценки вероятностей, описывается вектором сглаживания по формуле
Каждая компонента вектора меняется по закону простого экспоненциального сглаживания между нулем и единицей. Если вектор ( ) 1 − t p r вероятностный, то все его компоненты должны быть неотрицательными, и их сумма должна быть равна 1. Значение оценки p (t) k r есть результат экспоненциального сглаживания, и если распределение вероятностей наблюдений х(t) не меняется, то получаемые вероятности и будут действительными вероятностями k-го события. Если существует достаточно длительная реализация процесса, то начальные оценки со временем перестанут оказывать влияние (будут достаточно «взвешены»), и вектор сглаживания будет в среднем описывать вероятности и взаимно исключающих, и независимых событий. Значения компонент вектора u(t) r представляют собой выборку с биномиальным распределением, поэтому дисперсии k-й компоненты будут ( ) k k p pr r 1− . Дисперсия оценок k-и вероятности определяется соотношением |




|
|